Planificación - Geometría - El cono recto

Área: Matemática
Campo: Geometría
Contenido: Los cuerpos en revolución.
Aspecto: El cono recto (rotación de un triángulo rectángulo).
Propósito: Identificar las características del cono recto a partir de diferentes experiencias.
Antecedente: El cilindro recto.
Proyección: Superficie del cono recto.

Desarrollo:

• Dividir  la clase en cuatro grupos mediante un número asignado a cada uno.
• Explicar la consigna: cada grupo deberá pasar por las estaciones, comenzando en el número que les tocó y pasando al número siguiente de estación. Tendrán una consigna escrita que deberán de ejecutar en 5 minutos y llevarán consigo un cuaderno de campo para hacer las anotaciones que crean adecuadas.
• Leer las cuatro consignas para todos, evacuar dudas y comenzar con las actividades.

1. Estación #1: Realizar una experiencia con un palito y un triangulo rectángulo pegado al eje, el cual se irá girando. Los niños deben primero hipotetizar sobre cuál será la figura que se forme al girar y luego deberán de grabar su trayectoria.
2. Estación #2: Seguir las instrucciones (Anexo 2) para crear un cono en Geogebra, observar y explorar la figura 3D del cono recto. Pensar dónde podemos encontrar figuras similares en la vida real y dibujarlas en un papel.
3. Estación #3: Observar la figura 3D hecha en cartulina de un cono recto. Identificar entre varias opciones de desarrollos de diferentes figuras tridimensionales (Anexo 3), cuál sería la correcta para construir un cono recto.
4. Estación #4: Primero que nada, uno de los participantes del grupo deberá salir del salón, quedando excluido de la lectura de la tarea. Volverá con los ojos vendados  y los compañeros le colocarán la primer figura 3D pegada en la espalda y comenzarán a describir con características la figura, sin decir el nombre. El voluntario vendado deberá adivinar cuál es esa figura. Una vez que lo haga, cambiará la figura a adivinar. En uno de los dos turnos, deberá estar presente el cono recto. Una vez finalizado el juego, con la hoja del cono del equipo, los niños deberán escribir en su cuaderno cuáles son las partes que pueden distinguir en la figura.

• Al terminar la rotación entre las estaciones, volverán a sentarse en sus respectivos bancos.
• Socializar describiendo qué hicieron en cada estación, mostrando los resultados logrados (siguiendo el orden de las estaciones), y utilizando el pizarrón para llegar a una definición y a un análisis de las partes del cono recto para copiar en el cuaderno.  ¿Cuál fue la figura que trabajaron en todas las estaciones? ¿Qué características tiene? ¿Tiene caras? ¿A cuál otra figura trabajada anteriormente se parece? ¿Por qué? ¿Es un cuerpo de revolución? ¿Por qué?

Recursos:

• Televisión
• XO
• Figura geométrica triangular pegada a un lápiz
• Bufanda para utilizar a modo de venda
• Fotocopias con el nombre figuras para adivinar
• Cinta adhesiva
• Fotocopias con desarrollos de poliedros varios y cono recto

Estrategias:

• Uso de las TICs
• Material concreto
• Actividades lúdicas
• Trabajo en equipos
• Registro en cuaderno

Bibliografía

• ANEP (2008) Programa de educación inicial y primaria.
• ANEP (2016) Documento Base de análisis curricular.
• Chamorro M. (2006) "Didáctica de las Matemáticas para Primaria". España.
• Net Escuela. "Cono circular recto" Recuperado de: (https://neetescuela.org/cono-circular-recto/)
• Vitutor. "Cono". España. Recuperado de: (https://www.vitutor.com/geo/esp/f_6.html)
• Sangaku Maths. (2018) "Conos". Recuperado de: (https://www.sangakoo.com/es/temas/conos)
• Geogebra. "Comando cono". Recuperado de: (https://wiki.geogebra.org/es/Comando_Cono)

Justificación:
Teniendo en cuenta la fundamentación de la Secuencia Didáctica de Matemáticas, cuyo contenido enfocado en el campo de la Geometría es "Los cuerpos de revolución: Cilindro y Cono"; se intentará desarrollar varias actividades cortas para que los niños logren identificar las características del cono recto.

En este caso, también se intentan aplicar los principios del DUA, trabajados durante el año en Didáctica, aunque con la variable de que todos los niños pasarán por las diferentes actividades. De esta manera, además de tener en cuenta las inteligencias múltiples (Gardner) todos podrán comprender la geometría a partir de los diversos procesos que propone Chamorro: procesos de percepción, de representación, de construcción, de reproducción y de designación de los entes geométricos, en este caso el cubo recto.

La decisión de dividir la clase aleatoriamente responde a la necesidad de que no trabajen siempre los mismos niños juntos por afinidad y para utilizar el tiempo de manera más eficaz. El trabajo en equipo es ideal para potenciar la Zona de Desarrollo Próxima (Vygotski); así mismo, el uso de del material concreto para algunas actividades se fundamenta en la importancia de su utilización en el campo de las matemáticas que enfatiza Piaget.

Fundamentación:
En cuanto al Cono Recto per se, hay algunas definiciones y características que no pueden faltar en la institucionalización del conocimiento y, que en caso de que los niños no logren llegar a ellas, se explicarán, teniendo en cuenta la transposición didáctica (Chevallard) necesaria para un aprendizaje adecuado al nivel de la clase.

Definición de cono
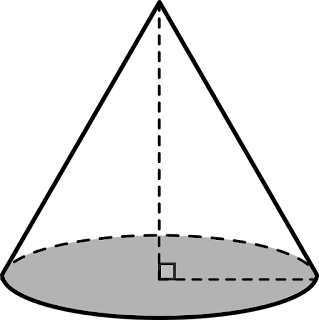
Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
Eje: 
Es el cateto fijo alrededor del cual gira el triángulo.
Bases: 
Es el círculo que forma el otro cateto.
Generatriz: 
Es la hipotenusa del triángulo rectángulo.
Altura: 
Es la distancia del vértice a la base.